Horospherical Learning with Smart Prototypes

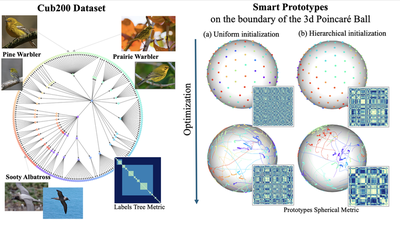
Hyperbolic spaces have emerged as an effective manifold to learn representations due to their ability to efficiently represent hierarchical data structures, with little distortion, even for low-dimensional embeddings. In the chosen hyperbolic model, such as the Poincaré ball, classification is usually conducted by leveraging a signed distance function to the hyperbolic equivalent of a plane (gyroplanes) or by measuring the alignment to a virtual fixed prototype. We propose, in a deep learning context, to leverage a different characterization of a decision boundary: Horospheres, which are level-sets of the Busemann function. They are geometrically equivalent to spheres tangent to the boundary of the hyperbolic space on a virtual point akin to a prototype. Accordingly, we define a new horospherical layer that can be adapted to any neural network backbone. In previous works, prototypes are usually uniformly distributed without using a potentially available label hierarchy for the task at hand. We also propose a hierarchically informed method for positioning these prototypes, based on the Gromov-Wasserstein distance. We find that the combination of a good initialization and optimization of the prototypes improves the baseline performance for image classification on hierarchical datasets and in two semantic segmentation tasks, conducted on image and point cloud datasets.